電子配置
目次
微小な世界の現象
原子や分子,電子などのような微小な世界の現象は,波が粒子のような性質をもったり,粒子の集団が波のような性質をもったりしている。また,エネルギーの値がとびとびだったり,正確な位置と運動が同時に求められなかったりと,目で見える世界の現象とは異なっている。このような世界の現象を表すのに量子力学が用いられる。
量子力学で電子配置を考える
量子力学では,いくつかの量子数(整数のようなとびとびの数)を使う。電子配置は,次の4つの量子数で指定できる。
- 主量子数 n=1,\;2,\;3,\;\cdots
- 方位量子数(軌道角運動量量子数) l=0,\;1,\;2,\;\cdots ,\;n-1
- 軌道磁気量子数 m_l=0,\;\pm 1,\;\pm 2,\;\cdots ,\;\pm l
- スピン磁気量子数 m_s=\pm 1/2 ▶補足① 電子スピンの発見
主量子数 n の値から,方位量子数 l ,軌道磁気量子数 m_l のとりうる値が決まる。たとえば,n=1 のとき l=0,\;m_l=0 になり,n=2 のとき l=0,\;1 で,l=0 では m_l=0,l=1 では m_l=0,\;\pm 1 になる。スピン磁気量子数は n とは関係なく,m_s=\pm 1/2 のいずれかである。
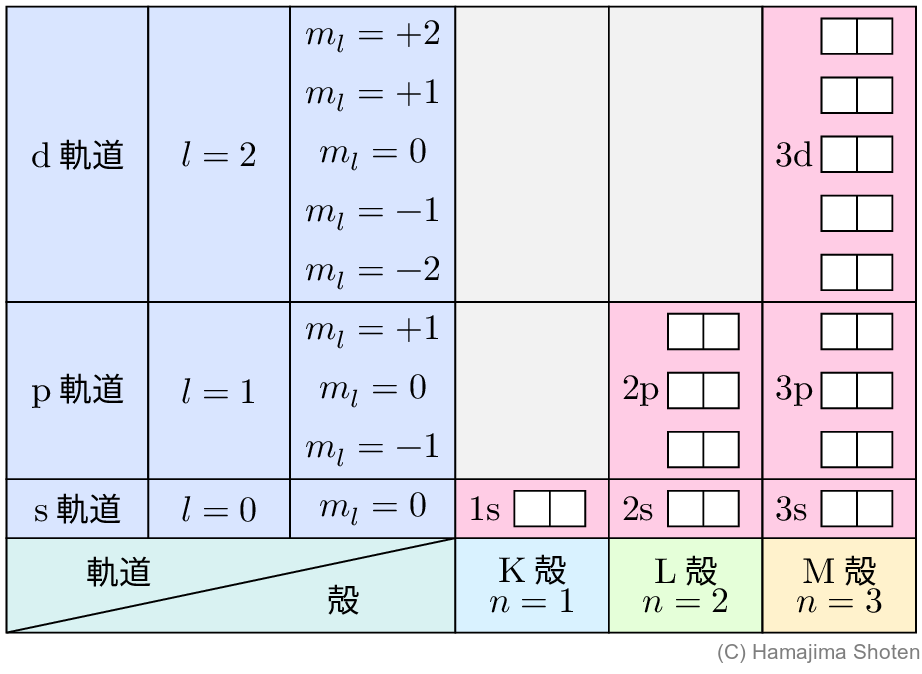
n=1,\;2,\;3,\;\cdots がそれぞれK殻,L殻,M殻,…,l=0,\;1,\;2,\;\cdots がそれぞれ \mathrm{s} 軌道,\mathrm{p} 軌道,\mathrm{d} 軌道,…に相当する。また,m_s=\pm 1/2は,1つの軌道に電子が2個まで収容できることを示す。
n=1,\;2,\;3 について整理すると,次のようになる。
構成原理
次の3つの規則(構成原理)が,原子の基底状態(エネルギーが最も低く安定した状態)における電子配置を決める指針になる。
1.エネルギーの低い軌道から
より低いエネルギーの軌道から先に,電子が入っていく。それぞれの軌道のエネルギーの序列は,次の通りである。 1\mathrm{s}<2\mathrm{s}<2\mathrm{p}<3\mathrm{s}<3\mathrm{p}<4\mathrm{s}<3\mathrm{d}<4\mathrm{p}<5\mathrm{s}<4\mathrm{d}<5\mathrm{p}<6\mathrm{s}<4\mathrm{f}<5\mathrm{d}<6\mathrm{p}<\cdots
2.各軌道に入る電子は2個まで(パウリの排他原理)
同じ軌道に入る電子は2個までで,2個の電子はスピン磁気量子数が異なる。
4つの量子数(主量子数 n,方位量子数 l,軌道磁気量子数 m_l,スピン磁気量子数 m_s )で見ると,これらがすべて同じ状態で存在できる電子は1個のみになる。これをパウリの排他原理という。これは,電子のような粒子(フェルミ粒子)に対して成り立つ(補足② スピン量子数)。
3.フントの規則
\mathrm{p} 軌道には3つの軌道 \mathrm{p}_x,\;\mathrm{p}_y,\;\mathrm{p}_z があり,これらは同じ殻ならエネルギーは等しい。このような軌道は,まず先に各軌道に1個ずつ電子が入っていく。また,それらの電子は同じスピン磁気量子数になっている。これをフントの規則という。
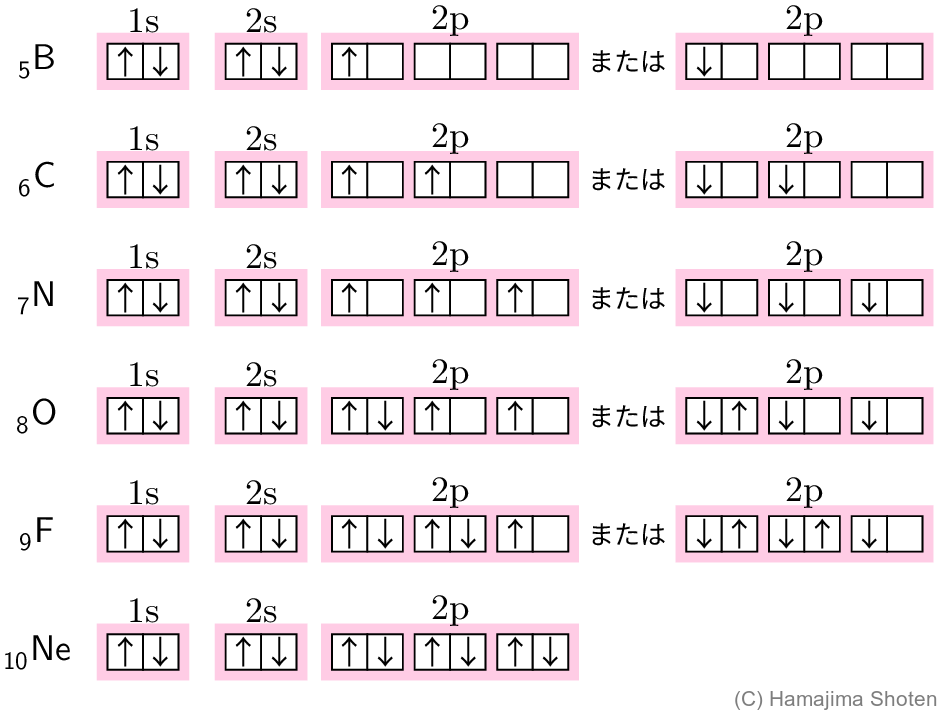
たとえば,2\mathrm{p} 軌道では,次のような順に電子が入っていく。なお,スピン磁気量子数 m_s=+1/2 を「↑」,m_s=-1/2 を「↓」で表した。
第4周期の元素
第4周期の元素の電子配置について考える。
4\mathrm{s} 軌道は,3\mathrm{d} 軌道よりエネルギーが低いため,構成原理1により,4\mathrm{s} 軌道から電子が入り,カリウム _{19}\mathsf{K},カルシウム \mathsf{_{20}Ca} の電子配置は,次のようになる。
- カリウム\mathsf{_{19}K} [\mathsf{Ar}]4\mathrm{s}^1
- カルシウム\mathsf{_{20}Ca} [\mathsf{Ar}]4\mathrm{s}^2
なお,軌道の右上の小さな数字はその軌道に入っている電子の数,[\mathsf{Ar}] はアルゴン \mathsf{_{18}Ar} の電子配置 1\mathrm{s}^22\mathrm{s}^22\mathrm{p}^63\mathrm{s}^23\mathrm{p}^6 を示す。
続くスカンジウム \mathsf{_{21}Sc} から亜鉛 \mathsf{_{30}Zn} までは [\mathsf{Ar}]3\mathrm{d}^N4\mathrm{s}^2 (スカンジウムが N=1,チタン \mathsf{Ti} が N=2,…)と表すことができる。たとえば,
- スカンジウム\mathsf{_{21}Sc} [\mathsf{Ar}]3\mathrm{d}^14\mathrm{s}^2
- チタン\mathsf{_{22}Ti} [\mathsf{Ar}]3\mathrm{d}^24\mathrm{s}^2
- バナジウム\mathsf{_{23}V} [\mathsf{Ar}]3\mathrm{d}^34\mathrm{s}^2
…
- 亜鉛\mathsf{_{30}Zn} [\mathsf{Ar}]3\mathrm{d}^{10}4\mathrm{s}^2
となる。
ただし,クロム \mathsf{_{24}Cr} と銅 \mathsf{_{29}Cu} は例外で,次のようになる。
- クロム\mathsf{_{24}Cr} [\mathsf{Ar}]3\mathrm{d}^54\mathrm{s}^1
- 銅\mathsf{_{29}Cu} [\mathsf{Ar}]3\mathrm{d}^{10}4\mathrm{s}^1
これは, 3\mathrm{d}^5,3\mathrm{d}^{10} のエネルギーが低い状態になるため,4\mathrm{s} 軌道の電子1個が 3\mathrm{d} 軌道に移ると考えられる。
ガリウム \mathsf{_{31}Ga} からは 4\mathrm{p} 軌道に電子が入っていく。
- ガリウム\mathsf{_{31}Ga} [\mathsf{Ar}]3\mathrm{d}^{10}4\mathrm{s}^24\mathrm{p}^1
- ゲルマニウム\mathsf{_{32}Ge} [\mathsf{Ar}]3\mathrm{d}^{10}4\mathrm{s}^24\mathrm{p}^2
- ヒ素\mathsf{_{33}As} [\mathsf{Ar}]3\mathrm{d}^{10}4\mathrm{s}^24\mathrm{p}^3
…
- クリプトン\mathsf{_{36}Kr} [\mathsf{Ar}]3\mathrm{d}^{10}4\mathrm{s}^24\mathrm{p}^6
電子配置と周期表
電子が軌道を満たしていく領域を,周期表上に色分けして示すと,次のようになる。

周期表の一定のブロックで,それぞれの軌道が電子で満たされていて,電子が満たされていく軌道の順がわかる。
補足
補足① 電子スピンの発見
コイルに電流を流すと磁場が生じるように,電子が運動すると磁場ができる。電子が軌道の中で運動(「電子の公転」)することによって,原子の中に磁気モーメント(極小の棒磁石のようなもの)ができる。これに相当する量子数が方位量子数 l,軌道磁気量子数 m_l である。
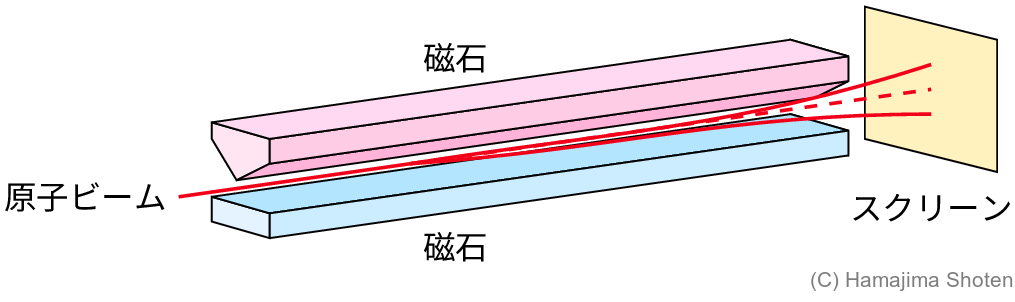
水素原子は,1\mathrm{s} 軌道に1個の電子をもつ。1\mathrm{s} 軌道は軌道磁気量子数 m_l=0 で,磁気モーメントをもたない。したがって,図4のような装置を使って,水素原子のビームを不均一磁場の中に通すと,まっすぐ進むはずである。ところが,水素原子のビームは2つに分裂した。
水素原子に発見された未知の磁気モーメントは,「電子の公転」に対して「電子の自転」(電子スピン)によるものと想定した。ただし,「電子の公転」や「電子の自転」は,あくまで目に見える世界の現象からの類推で,量子力学における現象はこれらとは違ったものである。
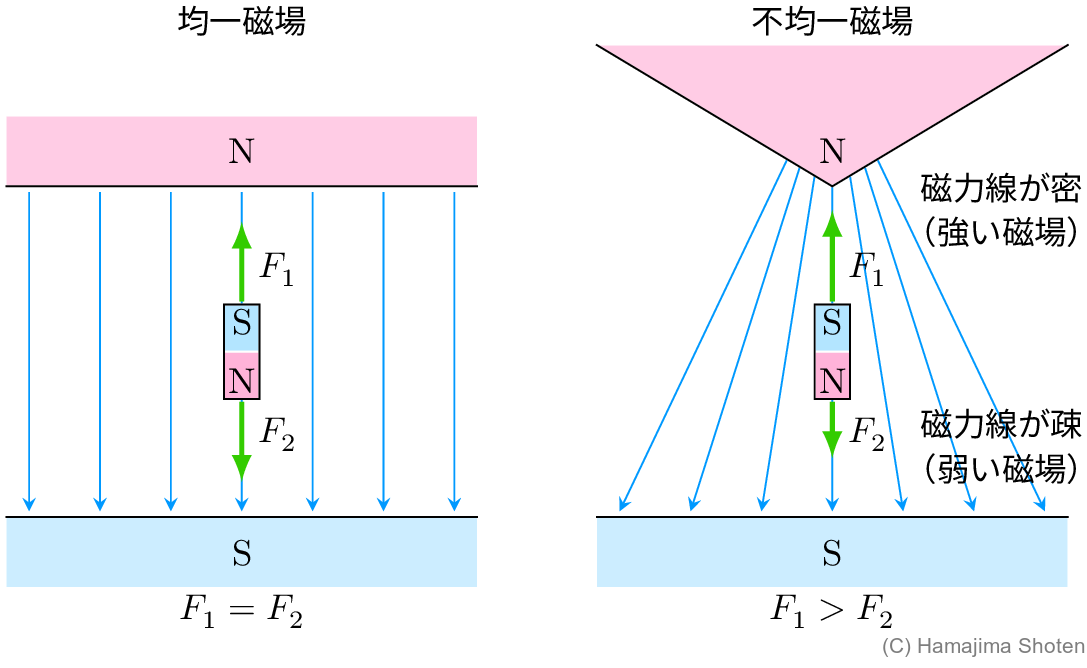
なお,均一磁場では,棒磁石に働く力がつり合ってしまうので,上側と下側とで磁場の強さが異なる不均一磁場を使う。
電子スピンの発見につながった「シュテルン-ゲルラッハの実験」(1922年)は,銀原子のビームを使ったものだったが,ここでは簡単にするため,水素原子のビームで説明した。
補足② スピン量子数(フェルミ粒子とボーズ粒子)
方位量子数 l と軌道磁気量子数 m_l に合わせて,スピン量子数 s とスピン磁気量子数 m_s を考えた。しかし,s=1 とすると,m_s=0,\;\pm 1の3つの状態ができてしまうが,電子スピンによる磁気モーメントは,実験からは2種類しかない。そこで,s=1/2,m_s=\pm 1/2 とした。
スピン量子数 s には,電子のように半整数になる粒子(フェルミ粒子)と,整数になる粒子(ボーズ粒子)とがある。パウリの排他原理はフェルミ粒子について成り立つ。