反応速度と温度の関係

アレニウスの式

反応速度定数 k と絶対温度 T\text{〔}\mathrm{K}\text{〕} には，次の関係が成り立ち，この式をアレニウスの式という。 \begin{align} k=Ae^{-\frac{E_\mathrm{a}}{RT}} \end{align} ここで，A は比例定数（頻度因子），e は自然対数の底，E_\mathrm{a} は活性化エネルギー，R は気体定数である。

アレニウスの式 (1) の両辺の自然対数をとると， \log_e k=\log_e Ae^{-\frac{E_\mathrm{a}}{RT}} となる。この右辺は， \log_e Ae^{-\frac{E_\mathrm{a}}{RT}} = \log_e A + \log_e e^{-\frac{E_\mathrm{a}}{RT}} = \log_e A - \frac{E_\mathrm{a}}{RT} なので，整理すると， \begin{align} \log_e k=-\frac{E_\mathrm{a}}{R}\frac{1}{T}+\log_e A \end{align} となる。式 (2) は，\log_e k\rightarrow y ，-\dfrac{E_\mathrm{a}}{R}\rightarrow a，\dfrac{1}{T}\rightarrow x，\log_e A\rightarrow bと対応させると，一次関数 y=ax+b\quad (a<0) になることがわかる。

例：ヨウ化水素の分解

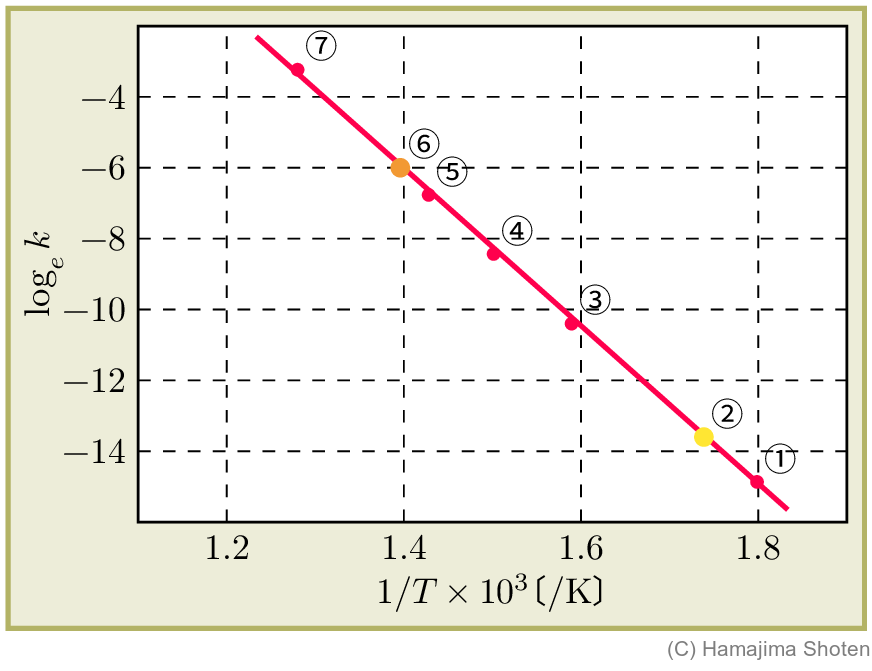
アレニウスのプロット

ヨウ化水素の分解 \mathsf{2\,HI\;\rightarrow \; H_2\;+\;I_2} について，さまざまな温度における反応速度定数を，次の表に示す。

	T\text{〔}\mathrm{K}\text{〕}	k\text{〔}\mathrm{L/(mol\cdot s)}\text{〕}	1/T\text{〔}\mathrm{/K}\text{〕}	\log_e k
① \bullet	556	3.52\times 10^{-7}	1.80\times 10^{-3}	-14.9
② \bullet	575	1.22\times 10^{-6}	1.74\times 10^{-3}	-13.6
③ \bullet	629	3.02\times 10^{-5}	1.59\times 10^{-3}	-10.4
④ \bullet	666	2.19\times 10^{-4}	1.50\times 10^{-3}	-8.43
⑤ \bullet	700	1.16\times 10^{-3}	1.43\times 10^{-3}	-6.76
⑥ \bullet	716	2.50\times 10^{-3}	1.40\times 10^{-3}	-5.99
⑦ \bullet	781	3.95\times 10^{-2}	1.28\times 10^{-3}	-3.23

これをグラフに表すと，図1のようになる。

活性化エネルギーを求める

上の表で，たとえば，T=575\,\mathrm{K}，T=716\,\mathrm{K} のときの値を，式 (2) に代入すると， \begin{align} -13.6 &= -\frac{E_\mathrm{a}}{R}\times 1.74\times 10^{-3}\,\mathrm{/K}+\log_e A\\ -5.99 &= -\frac{E_\mathrm{a}}{R}\times 1.40\times 10^{-3}\,\mathrm{/K}+\log_e A \end{align} となる。\text{式}(3)-\text{式}(4) から， \begin{align*} -13.6+5.99 &= (-1.74\times 10^{-3}\,\mathrm{/K}+1.40\times 10^{-3}\,\mathrm{/K})\times \frac{E_\mathrm{a}}{R}\\ E_\mathrm{a} &= \frac{(-13.6+5.99)R}{-1.74\times 10^{-3}\,\mathrm{/K}+1.40\times 10^{-3}\,\mathrm{/K}} \end{align*} が得られる。R=8.31\,\mathrm{J/(K\cdot mol)} として計算すると，活性化エネルギーを求めることができる。 E_\mathrm{a}\fallingdotseq 1.86\times 10^5\,\mathrm{J/mol}=1.86\times 10^2\,\mathrm{kJ/mol}