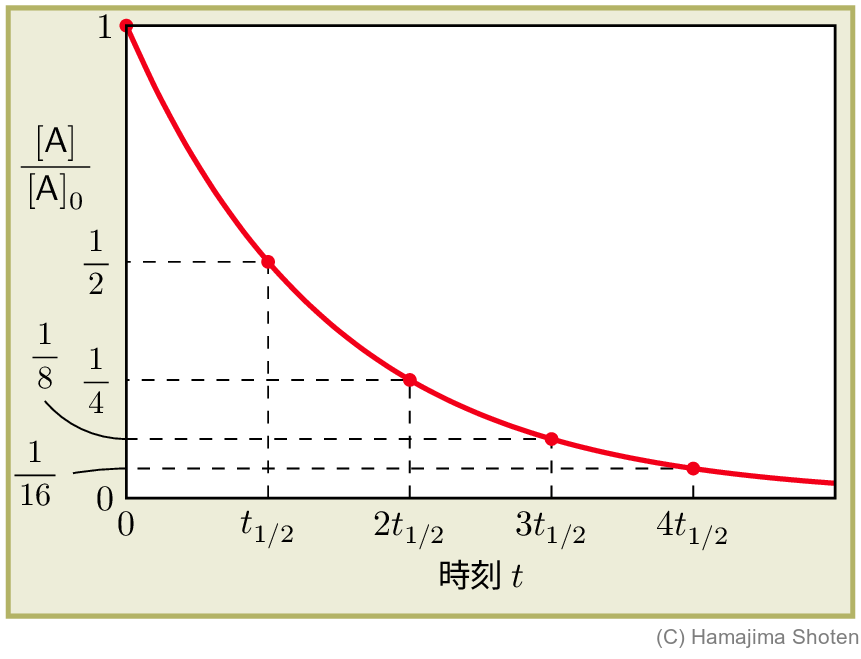
一次反応の半減期
目次
反応次数
\mathsf{A\;+\;B\;\rightarrow\;C\;+\;D} の反応速度式は, v=k\mathsf{[A]}^a\mathsf{[B]}^b となる。ただし,k は反応速度定数,\mathsf{[A]},\mathsf{[B]} はそれぞれ \mathsf{A},\mathsf{B} の濃度,a,b は実験で求める値である。
ここで,a+b を反応次数という。たとえば,次の例の \mathsf{N_2O_5} の分解反応は一次反応,\mathsf{NO_2} の分解反応は二次反応になる。 \begin{align*} & \mathsf{2\,N_2O_5\;\rightarrow\;4\,NO_2\;+\;O_2}&& v=k_1\mathsf{[N_2O_5]}\\ & \mathsf{2\,NO_2\;\rightarrow\; 2\,NO\;+\;O_2}&& v=k_2\mathsf{[NO_2]}^2 \end{align*}
一次反応の積分速度式
反応速度式が \begin{align} v=k\mathsf{[A]} \end{align} となる一次反応を考える。ただし,v は反応速度,k は反応速度定数,\mathsf{[A]} は反応物 \mathsf{A} の濃度を表す。
この反応速度は,\mathsf{[A]} の単位時間当たりの減少量になるので,時間 \Delta t の間に \mathsf{[A]} が\Delta \mathsf{[A]}変化したとすると,このときの平均の反応速度 \overline{v} は, \overline{v}=-\frac{\Delta \mathsf{[A]}}{\Delta t} である。時刻 t における瞬間の速度 v は,\Delta t を限りなく 0 に近づけたときの値なので, \begin{align} v=-\lim _{\Delta t\rightarrow 0}\frac{\Delta \mathsf{[A]}}{\Delta t}=-\frac{d\mathsf{[A]}}{dt} \end{align} となり,式 (1) と式 (2) から,次の式が成り立つ。 \begin{align} -\frac{d\mathsf{[A]}}{dt}=k\mathsf{[A]} \end{align}
時刻 0 のときの濃度(初濃度)を \mathsf{[A]}_0 ,時刻 t のときの濃度を \mathsf{[A]} として,式 (3) を変形し積分する。 \begin{align} -\frac{d\mathsf{[A]}}{\mathsf{[A]}} &= kdt\notag\\ -\int_{\mathsf{[A]}_0}^{\mathsf{[A]}}\frac{d\mathsf{[A]}}{\mathsf{[A]}} &= \int_{0}^{t}kdt \end{align} ここで,積分の公式 \int \frac{1}{x}dx=\log_e x +C,\:\int kdx=kx+C を利用すると,式 (4) は, -(\log_e \mathsf{[A]}-\log_e \mathsf{[A]}_0)=kt となる。対数関数の性質から,\log_e X -\log_e Y=\log_e \dfrac{X}{Y} だから, \begin{align} \log_e \frac{\mathsf{[A]}}{\mathsf{[A]}_0}=-kt \end{align} となる。 \log_e p=q のとき p=e^q だから,次の式が成り立つ。 \begin{align} \frac{\mathsf{[A]}}{\mathsf{[A]}_0}=e^{-kt}\quad\text{すなわち,} \mathsf{[A]}=\mathsf{[A]}_0e^{-kt} \end{align}
一次反応の半減期
濃度が初濃度 \mathsf{[A]}_0 の半分 \dfrac{1}{2}\mathsf{[A]}_0 になる時刻 t_{1/2} を半減期という。式 (5) に,\mathsf{[A]}=\dfrac{1}{2}\mathsf{[A]}_0,t=t_{1/2} を代入すると,左辺は, \log_e\frac{\;\dfrac{1}{2}\mathsf{[A]}_0\;}{\mathsf{[A]}_0}=\log_e\frac{1}{2}=\log_e 2^{-1}=-\log_e 2 であり,式 (5) は-\log_e 2=-kt_{1/2}となるので,次の式が成り立つ。 \begin{align} t_{1/2}=\frac{\log_e 2}{k} \end{align} この式から,一次反応の半減期は,初濃度によらず,反応速度定数で決まることがわかる。また,半減期がわかれば,反応速度定数を求めることができる。
例:五酸化二窒素の分解
五酸化二窒素が分解して,二酸化窒素と酸素になる反応 \mathsf{N_2O_5\;\rightarrow\;2\,NO_2\;+\;\frac{1}{2}\,O_2} は一次反応で,この反応速度 v は,反応速度定数を k,\mathsf{N_2O_5} の濃度を \mathsf{[N_2O_5]} とすると, v=k\mathsf{[N_2O_5]} と表される。この反応の 25\,{}^\circ\!\mathrm{C} における半減期が 1.03\times 10^4\,\mathrm{s} であった。式 (7) に,t_{1/2}=1.03\times 10^4\,\mathrm{s}を代入すると, 1.03\times 10^4\,\mathrm{s}=\frac{\log_e 2}{k} となるので,\log_e 2=0.693 とすると,反応速度定数 k は,次のようにして求めることができる。 k=\frac{\log_e 2}{1.03\times 10^4\,\mathrm{s}}=\frac{0.693}{1.03\times 10^4\,\mathrm{s}}\fallingdotseq 6.73\times 10^{-5}\,\mathrm{/s}
時刻 t と反応物の濃度の関係
v=k\mathsf{[A]} (式 (1) )で表される一次反応について,時刻 t と反応物の濃度比 \dfrac{\mathsf{[A]}}{\mathsf{[A]}_0} ( \mathsf{[A]}_0 は反応物の初濃度)の関係を考える。
この反応の半減期を t_{1/2} とすると,式 (6) により, \begin{align} t=t_{1/2}\text{のとき, }e^{-kt_{1/2}}=\frac{\mathsf{[A]}}{\mathsf{[A]}_0}=\frac{1}{2} \end{align} である。また, \begin{align*} t=2t_{1/2}\text{のとき, }&\frac{\mathsf{[A]}}{\mathsf{[A]}_0}=e^{-k\cdot 2t_{1/2}}=\left(e^{-kt_{1/2}}\right)^2=\left(\frac{1}{2}\right)^2=\frac{1}{4}\\ t=3t_{1/2}\text{のとき, }&\frac{\mathsf{[A]}}{\mathsf{[A]}_0}=e^{-k\cdot 3t_{1/2}}=\left(e^{-kt_{1/2}}\right)^3=\left(\frac{1}{2}\right)^3=\frac{1}{8}\\ t=4t_{1/2}\text{のとき, }&\frac{\mathsf{[A]}}{\mathsf{[A]}_0}=e^{-k\cdot 4t_{1/2}}=\left(e^{-kt_{1/2}}\right)^4=\left(\frac{1}{2}\right)^4=\frac{1}{16}\\ \cdots\cdots \end{align*} となり,時刻が半減期 t_{1/2} の2倍,3倍,4倍,…となると,\dfrac{\mathsf{[A]}}{\mathsf{[A]}_0} は \dfrac{1}{4},\dfrac{1}{8},\dfrac{1}{16},…となることがわかる。
この関係をグラフに表すと,次の図のようになる。