酵素反応の速度と阻害物質の作用(入試実例)
酵素反応の速度(ミカエリス・メンテンの式)と阻害物質の作用について,入試実例(2022年東京医科歯科大学)を解きながら解説する。
グレーバックの部分が入試からの引用で,今回のテーマと関係のない部分を一部割愛している。解答・解説は浜島書店が作成したものである。
(前段省略)
酵素反応の進行中は,一時的に酵素と基質が結合した酵素-基質複合体ができる。反応速度は,できた酵素-基質複合体の濃度に比例する。したがって,基質の濃度が大きくなると,酵素-基質複合体がつくられやすくなり,反応速度は増す。基質の濃度がさらに大きくなると,酵素-基質複合体の濃度は酵素の濃度に近づくが,酵素の濃度(上限値)をこえることはできず,反応速度も上限値(最大反応速度)に近づく。
酵素が触媒として働く生体内の化学反応では酵素( \mathsf{E} )は,基質( \mathsf{S} )と結合して酵素-基質複合体( \mathsf{ES} )となり,反応生成物( \mathsf{P} )を生じるが,\mathsf{ES} が \mathsf{E} と \mathsf{S} に分解する反応も起こる。これらの反応とそれぞれの反応速度式は,次のようになる。 \mathsf{E}\;+\;\mathsf{S}\;\overset{k_1}\rightleftarrows \!\!\!\!\!\!\! \underset{k_{-1}} {}\;\mathsf{ES} \;\overset{k_2}\rightarrow \mathsf{E}\;+\;\mathsf{P}\quad \cdots\cdots\text{①} \begin{align*} &\text{酵素反応} & &\text{反応速度}\\ &\mathsf{E}\;+\;\mathsf{S}\;\rightarrow \mathsf{ES} &&v_1=k_1\mathsf{[E]}\mathsf{[S]} &&\cdots\cdots\text{②}\\ &\mathsf{ES}\;\rightarrow \mathsf{E}\;+\;\mathsf{P} &&v_2=k_2\mathsf{[ES]} &&\cdots\cdots\text{③}\\ &\mathsf{ES}\;\rightarrow \mathsf{E}\;+\;\mathsf{S} &&v_{-1}=k_{-1}\mathsf{[ES]} &&\cdots\cdots\text{④}\\ \end{align*}
k_1,k_2 ,k_{-1} は,それぞれの反応の反応速度定数であり,\mathsf{[E]},\mathsf{[S]},\mathsf{[ES]} は,酵素,基質,酵素-基質複合体の濃度を表す。
\mathsf{ES} が分解する反応速度式 v_3 は,反応③と④が関与するので,反応速度定数を用いて次のようになる。 v_3=\text{( d )}\quad \cdots\cdots\text{⑤}
酵素反応の多くの場合,\mathsf{ES} の生成と分解はつりあい状態にあり,\mathsf{ES} の濃度は変化せず一定とみなすことができる。このような条件で,反応生成物 \mathsf{P} ができる反応速度 v_2 を考察してみよう。\mathsf{ES} の生成と分解は,つりあい状態にあるとき,v_1=v_3 であるから k_1\mathsf{[E]}\mathsf{[S]}=\text{( d )}\quad \cdots\cdots\text{⑥} となる。ここで,全酵素濃度を \mathsf{[E]}_\mathrm{t} (一定)とおく。全酵素濃度は,遊離の酵素の濃度と酵素-基質複合体の濃度の和であるので, \mathsf{[E]}_\mathrm{t}=\mathsf{[E]}+\mathsf{[ES]} \quad \cdots\cdots\text{⑦} である。式⑦に式⑥を代入して,\mathsf{[ES]} を \mathsf{[E]}_\mathrm{t} を用いて表すと, \mathsf{[ES]}=\text{( e )} ただし,K_\mathrm{m}=\dfrac{k_2+k_{-1}}{k_1} とすると, \mathsf{[ES]}=\text{( f )} となる。したがって,反応速度は, v_2=\frac{k_2\mathsf{[E]}_\mathrm{t}\mathsf{[S]}}{\mathsf{[S]}+K_\mathrm{m}} \quad \cdots\cdots\text{⑧} となる。
ある酵素 \mathsf{E} が基質 \mathsf{S} の加水分解反応に関与する酵素反応について,以下の実験を行った。さまざまな濃度の \mathsf{S} に一定濃度のEを加えて,37\,{}^\circ\!\mathrm{C} で反応を行った。その実験結果を表1に記す。基質の濃度は \mathrm{mmol/L},反応速度は\mathrm{mmol/(L\cdot min)}の単位で求めた。
表1 基質Sの加水分解実験の結果
| 反応前のSの濃度 \mathsf{[S]}\\\text{〔}\mathrm{mmol/L}\text{〕} | 反応速度v_2\\\text{〔}\mathrm{mmol/(L\cdot min)}\text{〕} | |
|---|---|---|
| 反応液1 | 0.083 | 0.0010 |
| 反応液2 | 0.167 | 0.0018 |
| 反応液3 | 0.417 | 0.0036 |
| 反応液4 | 0.833 | 0.0053 |
| 反応液5 | 1.667 | 0.0069 |
| 反応液6 | 4.167 | 0.0085 |
問1 (省略)
問2 d,e,fに当てはまる適切な文字式を記せ。ただし,dには反応速度定数を用いて記すこと。
dについては,v_3=v_2+v_{-1} だから, \begin{align} v_3=v_2+v_{-1}=k_2\mathsf{[ES]}+k_{-1}\mathsf{[ES]}=\underline{(k_2+k_{-1})\mathsf{[ES]}} \end{align} となり,式 (1) の下線部がdになる。
eとfについては,式⑦を変形して, \mathsf{[E]}=\mathsf{[E]}_\mathrm{t}-\mathsf{[ES]} とし,これを式⑥に代入すると, k_1(\mathsf{[E]}_\mathrm{t}-\mathsf{[ES]})\mathsf{[S]}=(k_2+k_{-1})\mathsf{[ES]} となる。これを \mathsf{[ES]} について解くと, \begin{align} \mathsf{[ES]}&=\frac{k_1\mathsf{[E]}_\mathrm{t}\mathsf{[S]}}{\;k_2+k_{-1}+k_1\mathsf{[S]}\;\;}\\ &=\frac{\mathsf{[E]}_\mathrm{t}\mathsf{[S]}}{\;\;\dfrac{k_2+k_{-1}}{k_1}+\mathsf{[S]}\;\;}\\ &=\frac{\mathsf{[E]}_\mathrm{t}\mathsf{[S]}}{\;\;K_\mathrm{m}+\mathsf{[S]}\;\;} \end{align} のようになり,式 (2) または式 (3) の右辺がe,式 (4) の右辺がfになる。
解答
d \bm{(k_2-k_{-1})\mathsf{[ES]}}
e \bm{\dfrac{k_1\mathsf{[E]}_\mathrm{t}\mathsf{[S]}}{\;k_2+k_{-1}+k_1\mathsf{[S]}\;\;}} または \bm{\dfrac{\mathsf{[E]}_\mathrm{t}\mathsf{[S]}}{\;\;\dfrac{k_2+k_{-1}}{k_1}+\mathsf{[S]}\;\;}}
f \bm{\dfrac{\mathsf{[E]}_\mathrm{t}\mathsf{[S]}}{\;\;K_\mathrm{m}+\mathsf{[S]}\;\;}}
問3 基質濃度 \mathsf{[S]} が大きく,\mathsf{[S]}\gg K_\mathrm{m}の場合,式⑧において,\mathsf{[S]}+K_\mathrm{m}\fallingdotseq \mathsf{[S]}とみなせるので,以下の式⑨が成り立つ。 v_2=k_2\mathsf{[E]}_\mathrm{t}\qquad \cdots\cdots\text{⑨} このときの v_2 は最大反応速度と考えられるので,V_\mathrm{max}=k_2\mathsf{[E]}_\mathrm{t} となる。
最大反応速度を V_\mathrm{max} とすると,式⑧と⑨から,v_2=\dfrac{V_\mathrm{max}}{2} のときの \mathsf{[S]} を求めよ。
V_\mathrm{max}=k_2\mathsf{[E]}_\mathrm{t} であることから,式⑧は, \begin{align} v_2=\frac{V_\mathrm{max}\mathsf{[S]}}{\mathsf{[S]}+K_\mathrm{m}} \end{align} となる。したがって, \begin{align} \frac{V_\mathrm{max}\mathsf{[S]}}{\mathsf{[S]}+K_\mathrm{m}}=\frac{V_\mathrm{max}}{2}\qquad \mathsf{[S]}=K_\mathrm{m} \end{align}
解答
\bm{\mathsf{[S]}=K_\mathrm{m}}
問4 (省略)
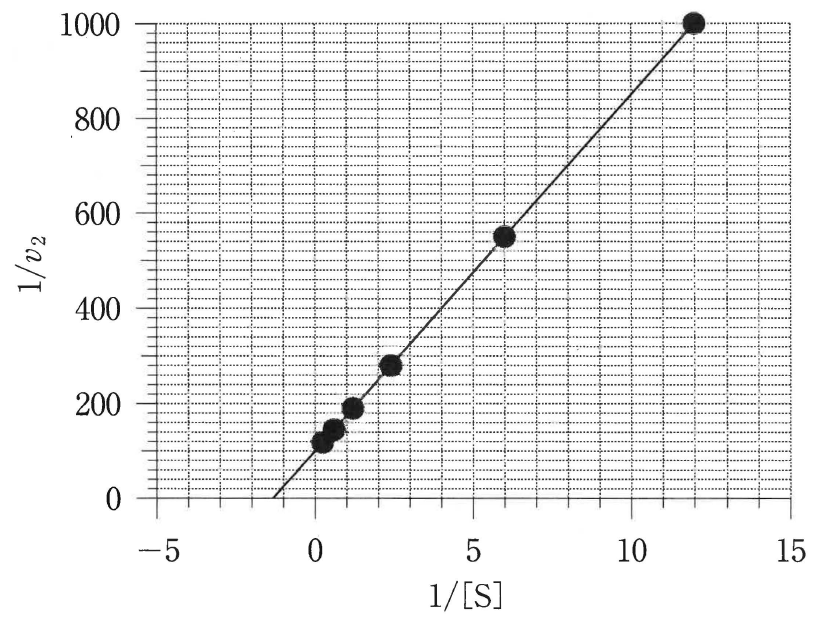
問5 基質濃度を \mathsf{[S]},反応速度を v_2,最大反応速度を V_\mathrm{max} とすると,式⑧の逆数および式⑨から,以下の式⑩が成り立つ。 \frac{1}{v_2}=\frac{K_\mathrm{m}}{V_\mathrm{max}\mathsf{[S]}}+\frac{1}{V_\mathrm{max}}\qquad \cdots\cdots\text{⑩} 式⑩と表2の逆数を用いて,縦軸を 1/v_2,横軸を 1/\mathsf{[S]} としてプロットを直線で結ぶと図の二重逆数プロットが得られた。図から,V_\mathrm{max} と K_\mathrm{m} を求めよ。
表2 表1の実験データ値の逆数
| 1/\mathsf{[S]} | 値 | 1/v_2 | 値 | |
|---|---|---|---|---|
| 1/0.083 | 12 | 1/0.0010 | 1000 | |
| 1/0.167 | 6.0 | 1/0.0018 | 550 | |
| 1/0.417 | 2.4 | 1/0.0036 | 280 | |
| 1/0.833 | 1.2 | 1/0.0053 | 190 | |
| 1/1.667 | 0.6 | 1/0.0069 | 145 | |
| 1/4.167 | 0.24 | 1/0.0085 | 118 |
図1 二重逆数プロット
図のグラフは点 (0,\;100) を通るので,切片は100\,\mathrm{(L\cdot min)/mmol}になる。式⑩から切片は 1/V_\mathrm{max} になるから, \frac{1}{V_\mathrm{max}} = 100\,\mathrm{(L\cdot min)/mmol} したがって, \begin{align} V_\mathrm{max} &= \frac{1}{100\,\mathrm{(L\cdot min)/mmol}}\notag\\ &= 0.01\,\mathrm{mmol/(L\cdot min)} \end{align} グラフは点 (12,\;1000) を通るので,グラフの傾きは, \frac{1000\,\mathrm{(L\cdot min)/mmol}-100\,\mathrm{(L\cdot min)/mmol}}{12\,\mathrm{L/mmol}-0\,\mathrm{L/mmol}}=75\,\mathrm{min} 式⑩から,グラフの傾きは,\dfrac{K_\mathrm{m}}{V_\mathrm{max}} だから, \begin{align} K_\mathrm{m}&=V_\mathrm{max}\times 75\,\mathrm{min}\notag\\ &=0.01\,\mathrm{mmol/(L\cdot min)}\times 75\,\mathrm{min}\notag\\ &=0.75\,\mathrm{mmol/L} \end{align}
解答
\bm{V_\mathrm{max} = 0.01}\,\mathbf{mmol/(L\cdot min)}
\bm{K_\mathrm{m}=0.75}\,\mathbf{mmol/L}
問6 酵素反応の場合,本来の基質ではなく,それと似た分子構造をもつ複合体を形成してしまうと,本来の基質とは結合できなくなる。このような物質を酵素阻害剤という。
上述した酵素実験の続きで,酵素阻害剤( \,\mathsf{I}\, )をあらかじめ添加することにより,酵素の一部が酵素-酵素阻害剤の複合体( \mathsf{EI} )になった。この阻害剤は,基質が結合した酵素-基質複合体に対しては直接的な影響を与えない。つまり,以下の化学平衡だけを考慮することになる。 \mathsf{E\;+\;I\;\rightleftarrows\;EI}\qquad \frac{\mathsf{[E]}\mathsf{[\,I\,]}}{\mathsf{[EI]}}=K_1 ここで酵素-阻害剤の解離反応の平衡定数を K_1 とした。
酵素阻害剤( \,\mathsf{I}\, )を添加した場合,式⑩は式⑪のように阻害剤の濃度 \mathsf{[\,I\,]} を用いて表される。 \frac{1}{v_2}=\frac{K_\mathrm{m}}{V_\mathrm{max}\mathsf{[S]}}\left(1+\frac{\mathsf{[\,I\,]}}{K_1}\right)+\frac{1}{V_\mathrm{max}}\qquad \cdots\cdots\text{⑪}
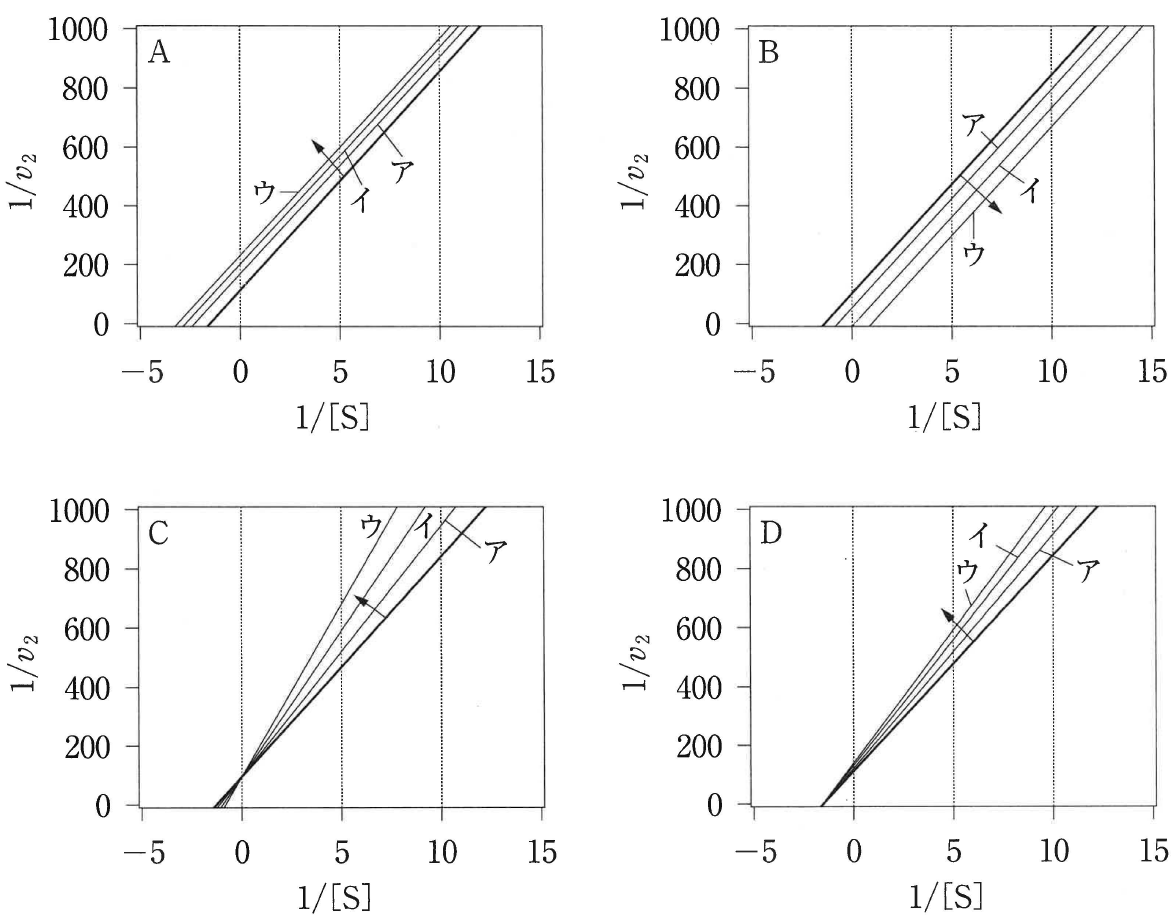
阻害剤の濃度をア,イ,ウの順番で上げていくと,図1で記した直線はどのように変わるか。図2のA〜Dの中から正しいものを一つ選べ。また,正しい理由を説明せよ。
図2
式⑪から,直線の傾きは \dfrac{K_\mathrm{m}}{V_\mathrm{max}}\left(1+\dfrac{\mathsf{[\,I\,]}}{K_1}\right),切片は \dfrac{1}{V_\mathrm{max}} なので,傾きは \mathsf{[\,I\,]} が大きくなると大きくなり,切片は \mathsf{[\,I\,]} に関わらず一定になる。したがって,Cのグラフの変化が正しいものになる。
解答
C