酵素反応の速度と阻害物質の作用
目次
生成物の生成速度式
ミカエリス・メンテンの式
基質が十分に存在していて,酵素-基質複合体が一定の濃度になっている状態(定常状態)を仮定し,生成物の生成速度を表す式(ミカエリス・メンテンの式)を導く。
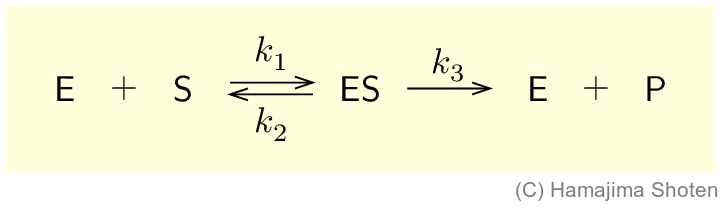
酵素(enzyme) \mathsf{E} は,その活性部位に基質(substrate) \mathsf{S} を結合させて,酵素-基質複合体 \mathsf{ES} をつくった後,生成物(product) \mathsf{P} と酵素 \mathsf{E} に分かれる。また,酵素-基質複合体 \mathsf{ES} は,酵素 \mathsf{E} と基質 \mathsf{S} に解離する逆反応も起こっている。この反応をまとめると,次のようになる。
k_1,k_2 ,k_3 は各反応の反応速度定数で,反応速度式は,それぞれ次のようになる。
\begin{align} & \mathsf{ES}\text{の生成速度 }&&v_1=k_1\mathsf{[E]}\mathsf{[S]}\\ & \mathsf{ES}\text{の分解速度}&&v_2=k_2\mathsf{[ES]}\\ & \mathsf{P}\text{の生成速度}&&v=k_3\mathsf{[ES]} \end{align}
ただし, \mathsf{E},\mathsf{S} ,\mathsf{ES},\mathsf{P} の濃度を,それぞれ \mathsf{[E]},\mathsf{[S]},\mathsf{[ES]},\mathsf{[P]} とした。また,生成物の生成速度に着目して,この速度を v とした。
\mathsf{ES} は,式 (1) の反応で生成,式 (2) と式 (3) の反応で分解,消費されるので, \begin{align} \mathsf{ES}\text{の正味の生成速度}=k_1\mathsf{[E]}\mathsf{[S]}-k_2\mathsf{[ES]}-k_3\mathsf{[ES]} \end{align} となる。
過剰の基質と酵素を混合すると,酵素-基質複合体の濃度は上昇して,すぐに一定の値(定常状態)になる。この定常状態では,\mathsf{ES} の正味の生成速度は 0 になるので,式 (4) から, \begin{align} k_1\mathsf{[E]}\mathsf{[S]}-k_2\mathsf{[ES]}-k_3\mathsf{[ES]}=0 \end{align} となる。これを \mathsf{[ES]} について解くと, \begin{align} \mathsf{[ES]}=\frac{k_1\mathsf{[E]}\mathsf{[S]}}{k_2+k_3}=\frac{\mathsf{[E]}\mathsf{[S]}}{\dfrac{k_2+k_3}{k_1}}=\frac{\mathsf{[E]}\mathsf{[S]}}{K_\mathrm{M}} \end{align} が得られる。ここで,\dfrac{k_2+k_3}{k_1}=K_\mathrm{M} とした。K_\mathrm{M} をミカエリス定数という。
\mathsf{[E]} は遊離している酵素の濃度,\mathsf{[ES]} は基質と結合している酵素の濃度を表しているので,酵素の全濃度を \mathsf{[E]_\mathrm{T}} とすると,\mathsf{[E]_\mathrm{T}}=\mathsf{[E]}+\mathsf{[ES]} となるので, \begin{align} \mathsf{[E]}=\mathsf{[E]_\mathrm{T}}-\mathsf{[ES]} \end{align} となる。式 (7) を式 (6) に代入すると, \mathsf{[ES]} = \frac{(\mathsf{[E]_\mathrm{T}}-\mathsf{[ES]})\mathsf{[S]}}{K_\mathrm{M}} となり,これを \mathsf{[ES]} について解くと, \begin{align} \mathsf{[ES]} = \frac{\mathsf{[E]_\mathrm{T}}\mathsf{[S]}}{\mathsf{[S]}+K_\mathrm{M}} \end{align} が得られる。式 (8) を式 (3) に代入すると,\mathsf{P} の生成速度 v を求めることができる。反応後すぐに定常状態になるので,この速度を反応の初速度 v_0 とすると,次のようになる。 \begin{align} v_0 = k_2\mathsf{[ES]} = \frac{k_2\mathsf{[E]_\mathrm{T}}\mathsf{[S]}}{\mathsf{[S]}+K_\mathrm{M}} \end{align}
基質が過剰にある( \mathsf{[S]}\gg K_\mathrm{M} )とき,\mathsf{[S]}+K_\mathrm{M}\fallingdotseq \mathsf{[S]}となり,このとき v_0 は最大になる。この値を V_\mathrm{max} とすると, \begin{align} V_\mathrm{max}=k_2\mathsf{[E]_\mathrm{T}} \end{align} となる。この式 (10) を式 (9) に代入すると,次の式が得られる。\begin{align} \bm{v_0 = \frac{V_\mathrm{max}\mathsf{[S]}}{\mathsf{[S]}+K_\mathrm{M}}}\qquad K_\mathrm{M}=\frac{k_2+k_3}{k_1}\text{(ミカエリス定数)} \end{align}
この式 (11) をミカエリス・メンテンの式という。この式は,基質濃度 \mathsf{[S]} と反応の初速度 v_0 の関係を表す。
基質濃度と生成速度
ミカエリス・メンテンの式から,基質濃度 \mathsf{[S]} と生成物の生成の初速度 v_0 の関係を表すグラフをつくり,その関係を考察する。
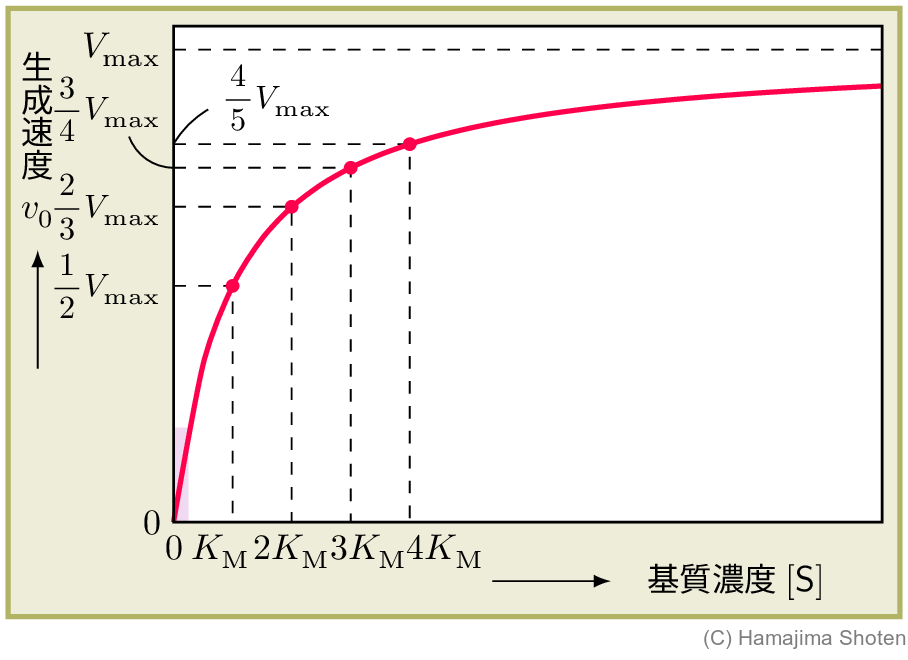
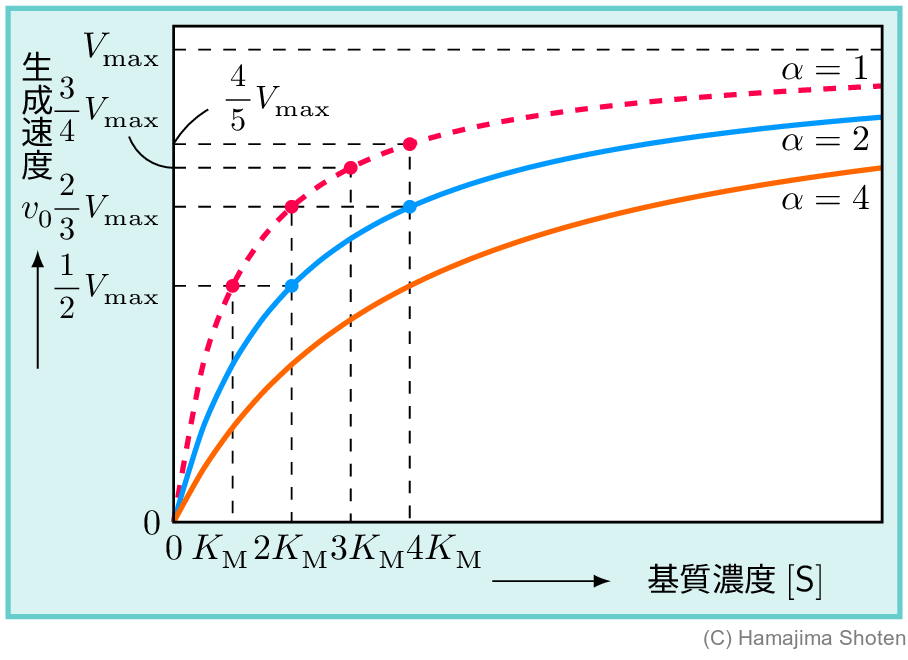
図1のグラフには,次のような関係がある。 \begin{align*} & \mathsf{[S]}=K_\mathrm{M}\text{のとき} && v_0=\dfrac{V_\mathrm{max}\times K_\mathrm{M}}{K_\mathrm{M}+K_\mathrm{M}}=\dfrac{1}{2}V_\mathrm{max}\\ & \mathsf{[S]}=2K_\mathrm{M}\text{のとき} && v_0=\dfrac{V_\mathrm{max}\times 2K_\mathrm{M}}{K_\mathrm{M}+2K_\mathrm{M}}=\dfrac{2}{3}V_\mathrm{max}\\ & \mathsf{[S]}=3K_\mathrm{M}\text{のとき} && v_0=\dfrac{V_\mathrm{max}\times 3K_\mathrm{M}}{K_\mathrm{M}+3K_\mathrm{M}}=\dfrac{3}{4}V_\mathrm{max}\\ & \cdots \end{align*}
また,基質が少ない( \mathsf{[S]}\ll K_\mathrm{M} )とき,\mathsf{[S]}+K_\mathrm{M}\fallingdotseq K_\mathrm{M}となるので, \begin{align} v_0=\frac{V_\mathrm{max}}{K_\mathrm{M}}\mathsf{[S]} \end{align} となり,基質が少ない場合,生成の初速度 v_0 は,基質濃度 \mathsf{[S]} に比例するとみなせる。これは,上のグラフの \mathsf{[S]} が小さい部分(たとえば,ピンク色の部分)を,ほぼ直線とみなすことに相当する。
ミカエリス・メンテンの式の変形
ミカエリス・メンテンの式の両辺を逆数にすると,酵素濃度 \mathsf{[S]} の逆数と初速度 v_0 の逆数の関係が直線の式になる。さまざまな \mathsf{[S]} における v_0 を測定して,その直線の式を決めると,最大速度 V_\mathrm{max} やミカエリス定数 K_\mathrm{M} を求めることができる。
ミカエリス・メンテンの式 (11) の両辺を逆数にすると, \begin{align} \frac{1}{v_0}=\frac{\mathsf{[S]}+K_\mathrm{M}}{V_\mathrm{max}\mathsf{[S]}}=\frac{K_\mathrm{M}}{V_\mathrm{max}}\cdot \frac{1}{\mathsf{[S]}}+\frac{1}{V_\mathrm{max}} \end{align} となる。式 (13) は,\dfrac{1}{v_0}\rightarrow y ,\dfrac{K_\mathrm{M}}{V_\mathrm{max}}\rightarrow a,\dfrac{ 1}{\mathsf{[S]}}\rightarrow x,\dfrac{1}{V_\mathrm{max}}\rightarrow b と対応させると,一次関数 {y=ax+b} になることがわかる。このように,逆数どうしをプロットする方法をラインウィーバー・バークのプロット(二重逆数プロット)という。
これをグラフに表すと,図2のようになる。
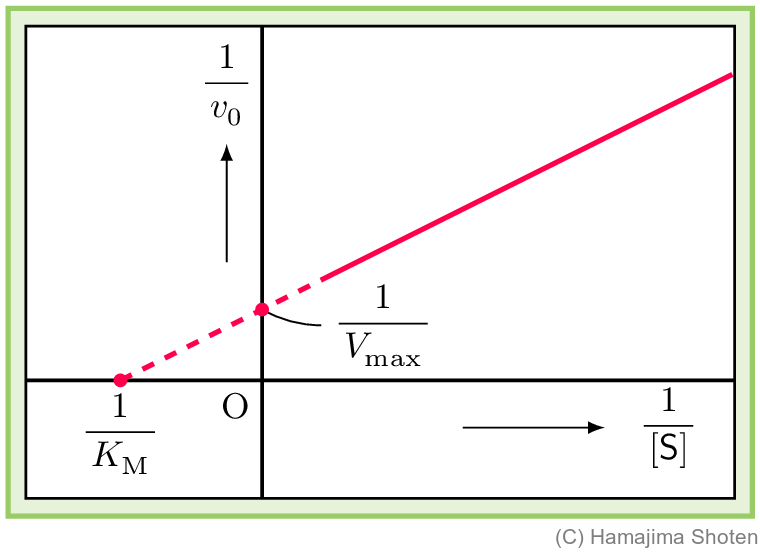
さまざまな基質濃度 \mathsf{[S]} における初速度 v_0 を実験で測定して,この直線の式を決めると,最大速度 V_\mathrm{max} やミカエリス定数 K_\mathrm{M} を求めることができる。
V_\mathrm{max} や K_\mathrm{M} が求まると,次のように定義される,酵素の触媒定数や触媒効率が得られる。
酵素の触媒定数 k_\mathrm{cat} は,次のように定義され,この値から酵素の活性を比較できる。 \begin{align} k_\mathrm{cat}=\dfrac{V_\mathrm{max}}{\mathsf{[E]_\mathrm{T}}}\qquad [E]_\mathrm{T}\text{は,酵素の全濃度} \end{align}
酵素の触媒効率 \eta は,次のように定義され,この値が大きいほど,酵素の効率は高い。 \begin{align} \eta =\dfrac{k_\mathrm{cat}}{K_\mathrm{M}} \end{align}
阻害物質の影響
酵素は,阻害物質によって,その働きが阻害されることがある。
競争的阻害
基質とよく似た構造をもつ阻害物質が酵素に結合すると,基質の酵素への結合が妨げられ,酵素反応が阻害される。
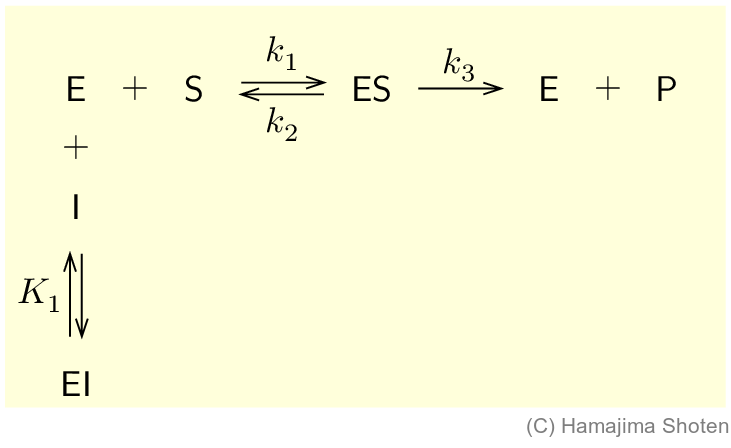
阻害物質(inhibitor) \mathsf{I} が,酵素 \mathsf{E} の活性部位に結合すると,基質 \mathsf{S} の結合が妨げられ,酵素の働きは低下する。このような阻害を競争的阻害という。
K_1 は,酵素と阻害物質が結合した複合体 \mathsf{EI} が分解するときの平衡定数で,次のようになる。 \begin{align} K_1=\frac{\mathsf{[E]}\mathsf{[\,I\,]}}{\mathsf{[EI]}}\qquad \text{よって,}\mathsf{[EI]}=\frac{\mathsf{[E]}\mathsf{[\,I\,]}}{K_1} \end{align}
酵素の全濃度は,式 (16) を利用して,次のように表すことができる。 \begin{align} \mathsf{[E]}_\mathrm{T} &= \mathsf{[E]}+\mathsf{[ES]}+\mathsf{[EI]}\notag\\ &= \mathsf{[E]}+\mathsf{[ES]}+\frac{\mathsf{[E]}\mathsf{[\,I\,]}}{K_1}\notag\\ &= \left(1+\frac{\mathsf{[\,I\,]}}{K_1}\right)\mathsf{[E]}+\mathsf{[ES]} \end{align} ここで, \begin{align} 1+\frac{\mathsf{[\,I\,]}}{K_1}=\alpha \end{align} とおき,式 (17) を \mathsf{[E]} について解くと, \begin{align} \mathsf{[E]}=\frac{\mathsf{[E]}_\mathrm{T}-\mathsf{[ES]}}{\alpha} \end{align} となる。阻害物質がない場合と同様に,酵素-基質複合体の濃度 \mathsf{[ES]} が一定の値(定常状態)になっているとすると,\mathsf{ES} の正味の生成速度は 0 になるので, \begin{align} k_1\mathsf{[E]}\mathsf{[S]}-k_2\mathsf{[ES]}-k_2\mathsf{[ES]} \end{align} だから, \begin{align} \mathsf{[E]}\mathsf{[S]}=\frac{k_2+k_3}{k_1}\mathsf{[ES]}=K_\mathrm{M}\mathsf{[ES]} \qquad \text{ただし,}\frac{k_2+k_3}{k_1}=K_\mathrm{M} \end{align} 式 (19) を式 (21) に代入して,\mathsf{[ES]} について解くと, \begin{align} \mathsf{[ES]}=\frac{\mathsf{[E]}_\mathrm{T}\mathsf{[S]}}{\mathsf{[S]}+\alpha K_\mathrm{M}} \end{align} となる。酵素の全濃度が \mathsf{[E]}_\mathrm{T},基質の濃度が \mathsf{[S]} のときの生成物生成の初速度 v_0 は,k_2\mathsf{[E]}_\mathrm{T}=V_\mathrm{max} (式 (10) )を利用すると,次のようになる。 \begin{align} v_0=k_2\mathsf{[ES]}=\frac{k_2\mathsf{[E]}_\mathrm{T}\mathsf{[S]}}{\mathsf{[S]}+\alpha K_\mathrm{M}}=\frac{V_\mathrm{max}\mathsf{[S]}}{\mathsf{[S]}+\alpha K_\mathrm{M}} \end{align} この式は,ミカエリス・メンテンの式(式 (11) )のミカエリス定数 K_\mathrm{M} に \alpha をかけた形になっている。
この式から,競争的阻害では,最大速度 V_\mathrm{max} は変化せず,ミカエリス定数が\alpha K_\mathrm{M}になることがわかる。また,\alpha=1 のとき,阻害物質がない場合に該当する。
たとえば,\alpha=2 のときを考えると, \begin{align*} & \mathsf{[S]}=K_\mathrm{M}\text{で}&&v_0=\frac{V_\mathrm{max}\times K_\mathrm{M}}{K_\mathrm{M}+2K_\mathrm{M}}=\frac{1}{3}V_\mathrm{max}\\ & \mathsf{[S]}=2K_\mathrm{M}\text{で}&&v_0=\frac{V_\mathrm{max}\times 2K_\mathrm{M}}{2K_\mathrm{M}+2K_\mathrm{M}}=\frac{1}{2}V_\mathrm{max}\\ & \mathsf{[S]}=3K_\mathrm{M}\text{で}&&v_0=\frac{V_\mathrm{max}\times 3K_\mathrm{M}}{3K_\mathrm{M}+2K_\mathrm{M}}=\frac{3}{5}V_\mathrm{max}\\ & \mathsf{[S]}=4K_\mathrm{M}\text{で}&&v_0=\frac{V_\mathrm{max}\times 4K_\mathrm{M}}{4K_\mathrm{M}+2K_\mathrm{M}}=\frac{2}{3}V_\mathrm{max}\\ & \cdots\cdots \end{align*} となる。\alpha=1 (阻害物質がない場合)と \alpha=2,\alpha=4 について,グラフに表すと図3のようになる。
競争的阻害のラインウィーバー・バークのプロット
競争的阻害がある場合のミカエリス・メンテンの式 (23) の両辺を逆数にすると, \begin{align} \frac{1}{v_0}=\frac{\alpha K_\mathrm{M}}{V_\mathrm{max}}\cdot \frac{1}{\mathsf{[S]}}+\frac{1}{V_\mathrm{max}} \end{align} となる。これをグラフに表すと,図4のようにある。
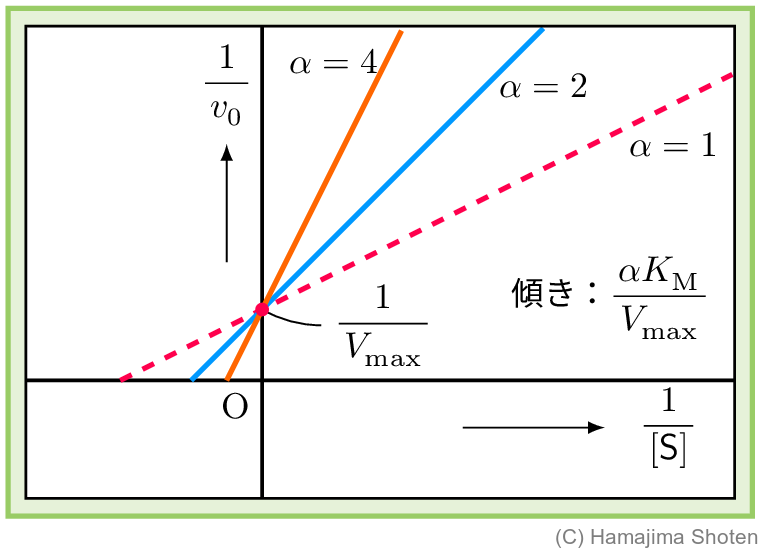
競争的阻害のラインウィーバー・バークのプロットによる直線は,\alpha によって傾きが変化するが,切片は変わらないので V_\mathrm{max} は一定である。
混合した阻害
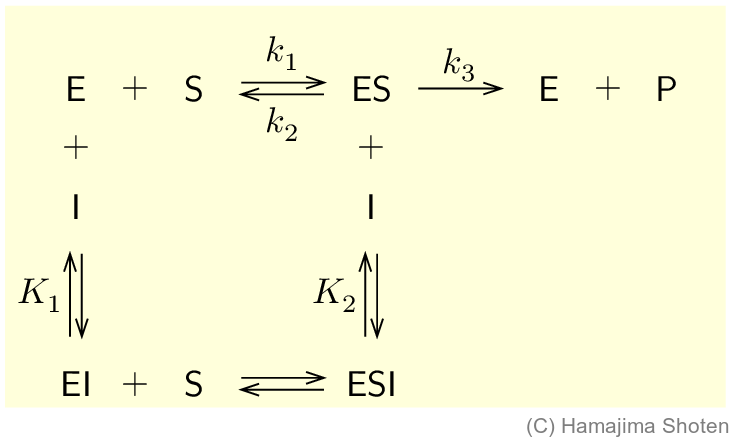
阻害物質が,酵素にも酵素-基質複合体にも結合して,酵素の働きを阻害する場合を考える。
阻害物質 \mathsf{I} が酵素-基質複合体 \mathsf{ES} に結合して,酵素の働きを阻害する場合を不競争的阻害(あとに説明する非競争的阻害とは異なる)という。この場合,\mathsf{I} は酵素 \mathsf{E} の活性部位以外に結合する。さらに,阻害物質 \mathsf{I} が,酵素単体にも酵素-基質複合体にも結合するような混合した阻害について考える。
この場合,生成物の生成初速度 v_0 は,次のようになる。 \begin{align} v_0=\frac{V_\mathrm{max}\mathsf{[S]}}{\alpha K_\mathrm{M}+\alpha ^\prime \mathsf{[S]}}\qquad \text{ここで,} \alpha =1+\frac{\mathsf{[\,I\,]}}{K_1}\text{,}\alpha ^\prime =1+\frac{\mathsf{[\,I\,]}}{K_2} \end{align}
このような混合した阻害のうち,\alpha = \alpha ^\prime,つまり K_1=K_2 のときを考えると,式 (25) は, \begin{align} v_0=\frac{V_\mathrm{max}\mathsf{[S]}}{\alpha K_\mathrm{M}+\alpha \mathsf{[S]}}=\frac{V_\mathrm{max}/\alpha \mathsf{[S]}}{K_\mathrm{M}+\mathsf{[S]}}=\frac{V_\mathrm{max}^\prime \mathsf{[S]}}{K_\mathrm{M}+\mathsf{[S]}} \end{align} となる。ただし,V_\mathrm{max}^\prime =\dfrac{V_\mathrm{max}}{\alpha} とした。この式から,V_\mathrm{max} は変わるが,K_\mathrm{M} は変わらないことがわかる。このような阻害を非競争的阻害という。これは,先に説明した不競争的阻害とは異なる。