金属の結晶格子
図は,ある金属の結晶の単位格子である。
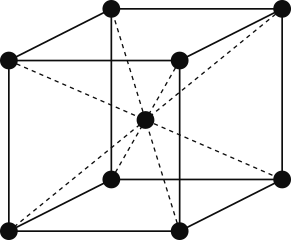
(1) この結晶構造を何というか。
(2) この結晶中で,1個の原子に接している原子は何個か。
(3) この単位格子中に含まれる原子は何個か。
(4) この金属の密度をd〔g/cm3〕,単位格子の一辺の長さをa〔cm〕として,金属原子1個の質量m〔g〕を,d,a を用いて表せ。
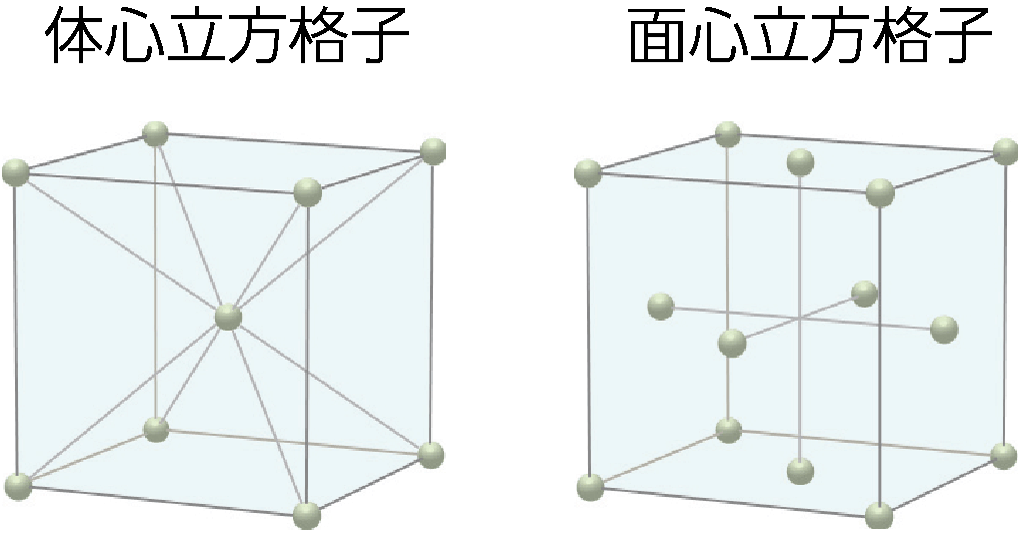
体心立方格子
立方体の中心と各頂点に原子が配列
面心立方格子
立方体の各面の中心と,各頂点に原子が配列
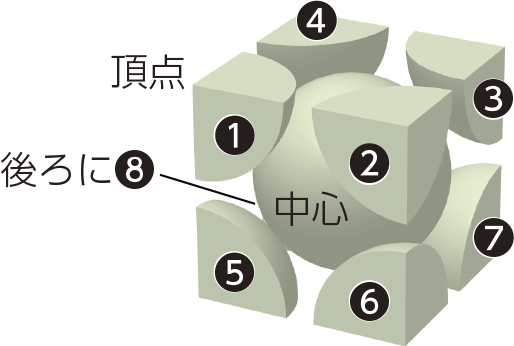
体心立方格子
中心の原子は各頂点の原子と接している。
★体心立方格子を回転させてみよう!
8個
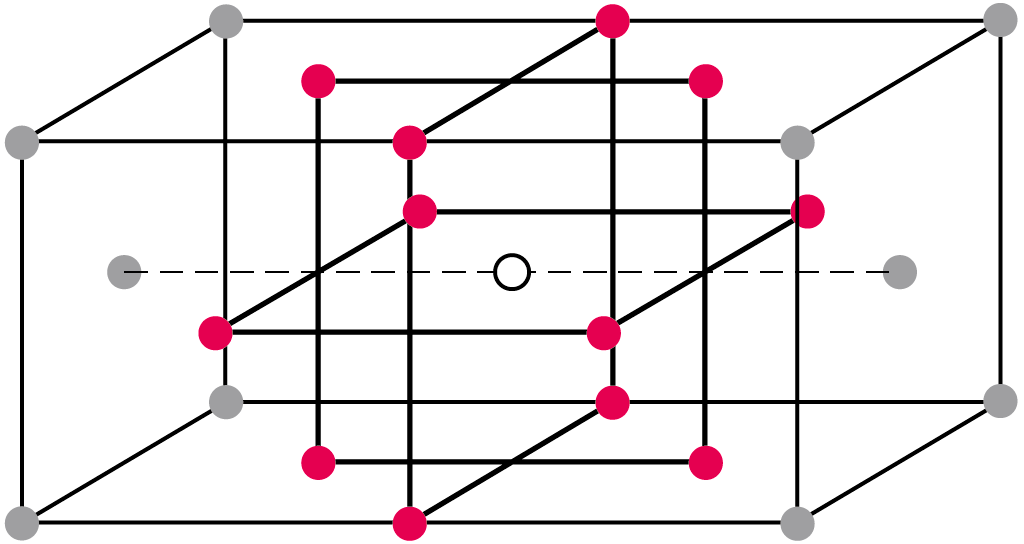
2つの単位格子をつなげると,○の原子は●の原子12個に接している。
単位格子中には,各頂点にある8つの原子は\(\dfrac{1}{8}\)個ずつ,
中心の原子は1個含まれる。
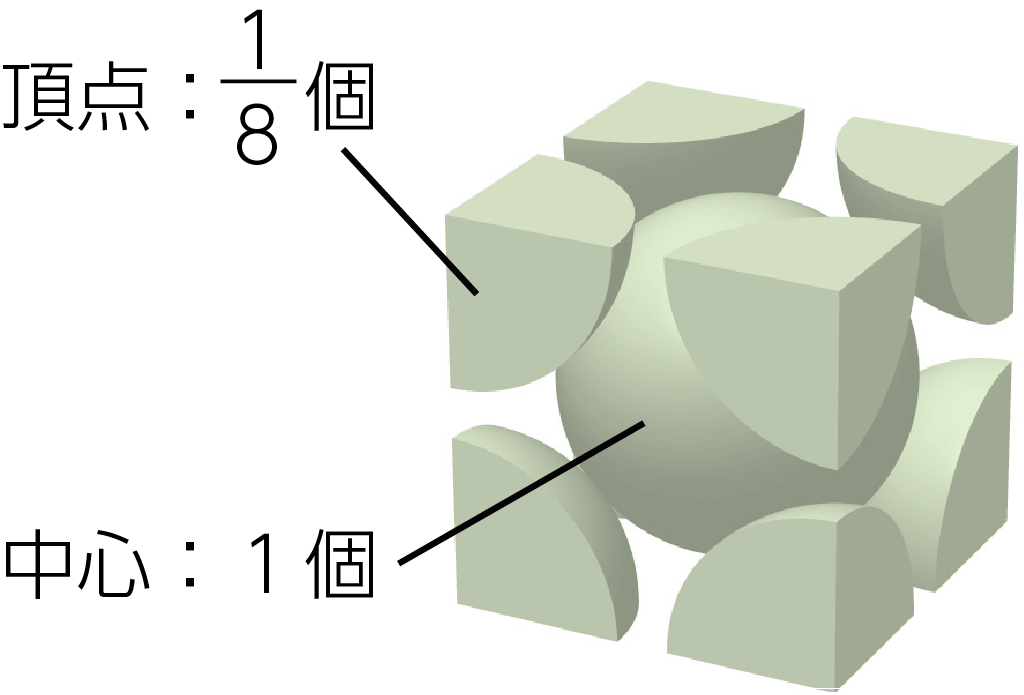
\[ \begin{matrix} {\dfrac{1}{8} \times 8} & + & {1} & = 2 \\ {\color{dodgerblue} 頂点} & & {\color{dodgerblue} 中心} & \end{matrix} \]
2個
単位格子中には,各頂点にある8つの原子は\(\dfrac{1}{8}\)個ずつ,各面の中心にある6つの原子は\(\dfrac{1}{2}\)個ずつ含まれている。
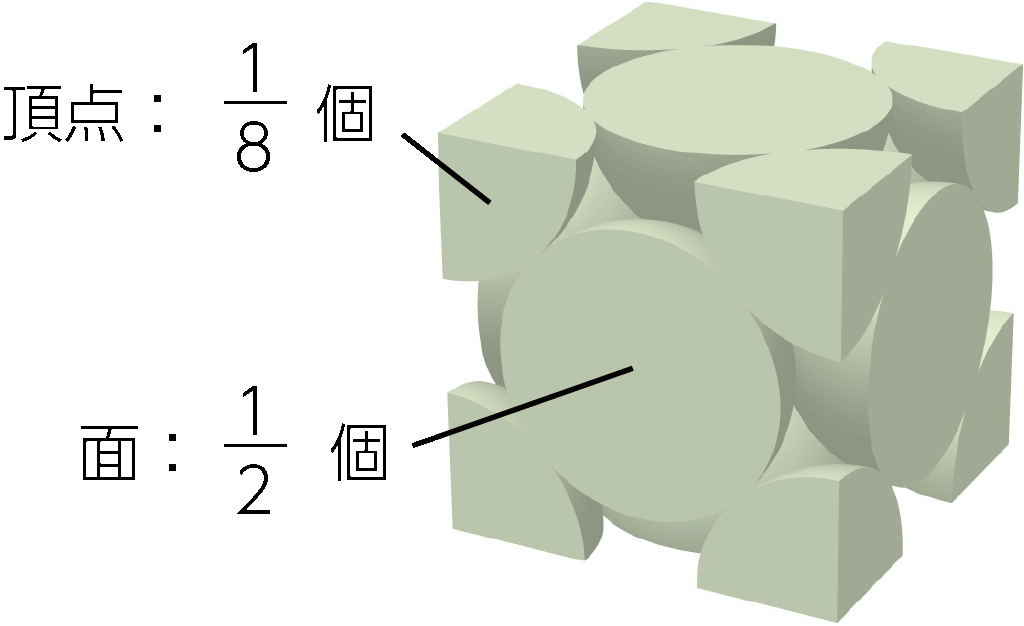
\[ \begin{matrix} {\dfrac{1}{8} \times 8} & + & {\dfrac{1}{2} \times 6} & = 4 \\ {\color{dodgerblue} 頂点} & & {\color{dodgerblue} 中心} & \end{matrix} \]
密度
一定体積当たりの質量。
密度(g/cm3)=質量(g)÷体積(cm3)
→質量(g)=密度(g/cm3)×体積(cm3)
単位格子の質量は,
金属の密度×単位格子の体積
単位格子には,⑶より,2個の原子が含まれるので,原子1個の質量m〔g〕は,
\[ \begin{split} & {\color{dodgerblue} 密度} {\color {dodgerblue} 単位格子の体積}\\ m \mathrm{〔g〕} & = \dfrac{{d\mathrm{〔g/cm^3〕} \times (a \mathrm{〔cm〕})^3}}{{2}}\\ & {\color {dodgerblue} 単位格子の質量}\\ & = \dfrac{d\mathrm{〔g/cm^3〕} \times a^3\mathrm{〔cm^3〕}}{{2}}\\ & {\color {dodgerblue} 単位格子に含まれる原子の数} \end{split} \]
\(\dfrac{a^3 d}{2}\)
※一般に,文字はアルファベット順に書く。
単位格子の質量は,
金属の密度×単位格子の体積
単位格子には4個の原子が含まれるので, 原子1個の質量m〔g〕は,
\[ \begin{split} &{\color {dodgerblue} 単位格子の質量}\\ m & = \dfrac{{d \times a^3}}{{4}}\\ &{\color {dodgerblue} 単位格子に含まれる原子の数}\\ &= \dfrac{a^3 d}{4} \end{split} \]